[머신러닝] K-Means 군집화

K-Means 알고리즘 :  

 

데이터 포인트들을 비슷한 속성의 그룹으로 묶어주는 비지도학습 알고리즘 중 하나이다.

 

• 'Centroid'라는 클러스터(군집)의 중심점 개념이 사용된다. 
• 데이터 포인트들과 Centroid들 간 거리 계산을 통해 Centroid들의 위치가 재설정되며 학습이 진행된다. 

이 시간에는 K-Means 알고리즘 수행 단계를 간단히 정리해보고자 한다. 

---

K-Means 알고리즘 수행 단계 

'초기화', '학습', '새로운 데이터에 적용' 이렇게 크게 3단계로 구분할 수 있다. 

 

1. 초기화

사용자가 처음 정하는 아래 2개 항목은 알고리즘 수행 결과에 큰 영향을 미친다.  

• 클러스터 개수 : 최종적으로 만들고자 하는 클러스터의 개수를 정해준다. 
• 클러스터 중심점(Centroid) 위치 설정 방법 : 중심점의 처음 위치 설정 방법을 정해준다.   
  * Random Partition, Forgy 방법 등 처음 중심점 위치를 설정하는 여러 방법이 있으며, sklearn.cluster.KMeans 모듈에서는 클러스터 간 거리를 최대한 떨어뜨리는 k-means++ 방법이 디폴트로 설정되어 있다. 

군집화 전 데이터 포인트들의 모습

군집 수를 3개로 정하고 랜덤하게 군집 중심(Centroid)들을 배치한 모습 (x로 표시)

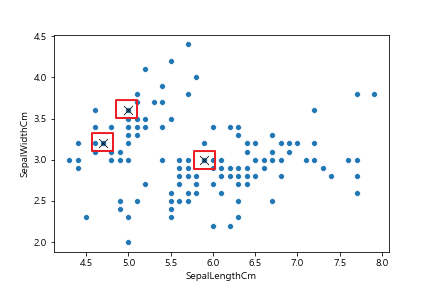
2. 학습 

데이터 포인트들과 Centroid들 간 유클리드 거리를 계산하며 Centroid들의 위치를 계속 수정한다. 

 

   1) 각각의 데이터 포인트 \(x_i\) 와 Centroid 간 유클리드 거리를 계산한다. 

모든 데이터 포인트 \(x_i\)에 대해 최소 거리를 계산

   2) 가장 짧은 거리의 Centroid로 데이터 포인트를 할당한다.

모든 데이터 포인트들을 가까운 군집(클러스터)에 할당한 모습

 

   3) 데이터 포인트들의 배정이 끝난 후, Centroid들을 배정된 데이터 포인트의 평균값으로 이동시킨다.

(왼쪽) Centroid 위치 변경 전 (오른쪽) 데이터 포인트들의 평균 값으로 Centroid 위치 변경 후

 

   4) Centroid들이 더 이상 움직이지 않을 때까지 반복한다.

변경된 Centroid 위치로 다시 거리를 계산하여 클러스터에 할당

Centroid 위치가 변경되지 않을 때까지 반복

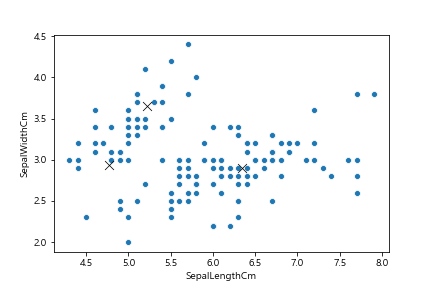
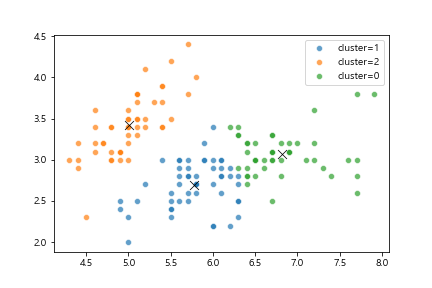
* 유클리드 거리는 곡선을 가진 공간에서 사용하기에 적합하지 않으며, K-Means 클러스터링이 적용되는 공간은 평평하다고 가정한다.

 

3. 새로운 데이터에 적용 

학습에 사용되지 않은 데이터 포인트들에 대해서도 학습된 K-Means 모델을 적용하여 어떤 군집에 속하는지 알 수 있어야 한다. 학습 때와 마찬가지로, 데이터 포인트들과 각 클러스터의 중심(Centroid) 간 거리를 계산하여 가장 가까운 클러스터로 해당 데이터 포인트를 배정한다.

 

반응형

---

K-Means 알고리즘의 장점 

• 알고리즘이 쉽고 간결하다.
• 클러스터링 알고리즘 중에서 비교적 빠르게 수행된다. 

 

K-Means 알고리즘의 단점  

• local minima에 빠지기 쉬워서 반복 수행해야 한다. 
• 속성의 개수가 많을수록 군집화의 정확도가 떨어진다. (차원의 저주) 
• 초기값에 영향을 많이 받고, outlier에 취약하다.

 

 

참고자료 

• 파이썬 머신러닝 완벽 가이드(권철민 저) 인프런 온라인 강의 
• 알고리즘 중심의 머신러닝 가이드(스티븐 마슬랜드 저/강전형 역) 도서
• scikit-learn 클러스터링 모듈 관련 문서