이전 포스팅에서는 S.O.M 알고리즘의 수행 단계와 평가 지표에 대해 알아보았다.
2021.05.04 - [머신러닝] - S.O.M 알고리즘 (1) - 개념
이번에는 SOM을 numpy 기반으로 작게 구현해 놓은 MiniSom 패키지를 활용하여 클러스터링과 시각화를 해볼 것이다.
0. 실습 준비
- MiniSom 패키지를 설치한다.
pip을 이용하여 tensorflow라는 이름의 anaconda 가상환경에 패키지를 설치한다.
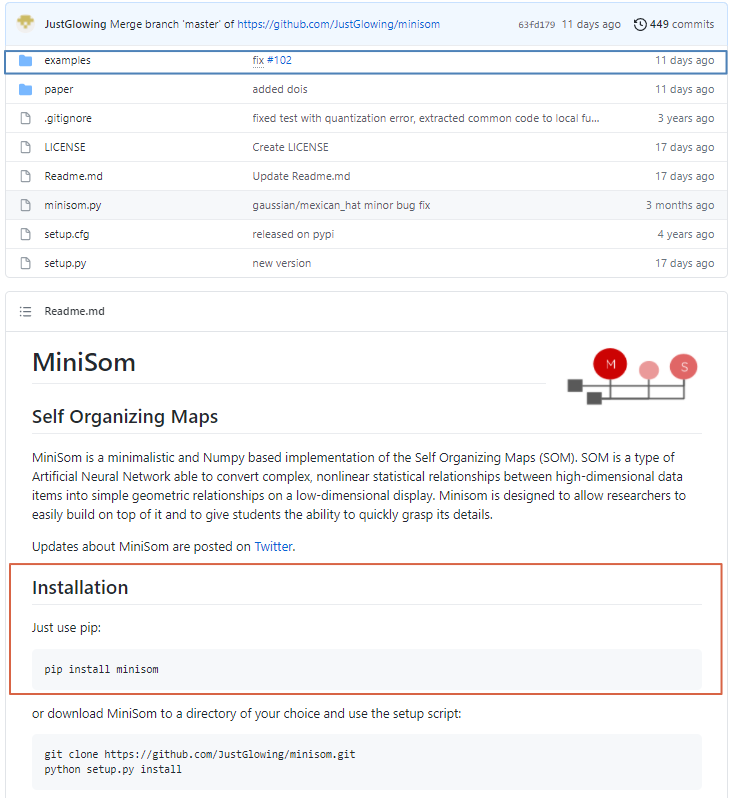
* github 페이지 'examples' 폴더에서 패키지의 다양한 활용 예시 코드를 볼 수 있으며, 'minisom.py' 코드를 통해 SOM 알고리즘이 어떻게 구현되어 있는지 확인할 수 있다.
1. Jupyter notebook으로 데이터 로드
클러스터링은 비지도 학습의 한 종류이므로, iris 데이터셋 target 값에 해당하는 'Species'컬럼은 사용하지 않는다.
150개의 행, 4개의 컬럼으로 데이터프레임이 구성된다.
df_iris = pd.read_csv('Iris.csv')
df_iris.drop('Id',axis=1,inplace=True)
#data_y는 target값 -> 사용하지 않음
data_y = df_iris[['Species']]
#모델 생성 및 시각화에 활용할 데이터프레임
data = df_iris.iloc[:,:-1]
#데이터셋 확인
data.shape
data.head(10)
2. Z-score 정규화
모든 설명변수를 동일한 정도의 스케일로 모델에 반영하기 위한 단계이다.
각 컬럼의 5-number summary 값을 먼저 도출하여 스케일의 차이를 확인하고 Z-score 정규화를 수행한다.
#각 컬럼의 요약 값 확인
data.describe()
data.head(5)
#표준정규분포를 활용한 Normalization 수행
data = (data-np.mean(data,axis=0))/np.std(data,axis=0)
#데이터셋 확인
data.shape
data.head(5)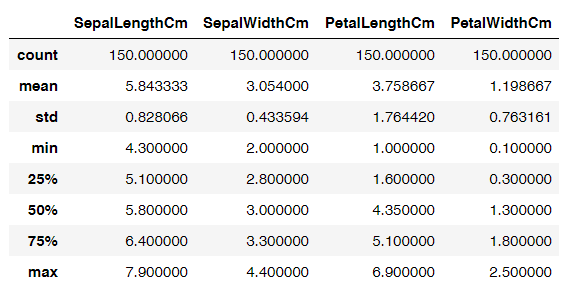

3. 모델 생성 및 비교
하이퍼 파라미터를 다양하게 조합해서 모델을 생성하고, 모델별 QE(Quantization Error)값과 클러스터 개수 정보가 담긴 데이터프레임을 생성한다.
* MiniSom 패키지에서 SOM모델의 topology를 'hexagonal'로 선택하는 경우 TE(Topographic Error)값 계산은 지원하지 않는다.
본 실습에서는 맵 사이즈, neighborhood의 반경, 학습률, 초기값 설정 방법(random, pca)만 활용해서 파라미터 조합을 생성했다.
s_time = pd.Timestamp.now()
print('시작시간:',s_time,'\n')
#원하는 파라미터 조합 리스트화
map_n= [n for n in range(2,6)]
para_sigma= [np.round(sigma*0.1,2) for sigma in range(1,10)]
para_learning_rate= [np.round(learning_rate*0.1,2) for learning_rate in range(1,10)]
#결과 값을 담을 리스트 res 생성
res = []
#모든 조합에 대해 모델 생성 및 qe,te값 계산
for n in map_n:
for sigma in para_sigma:
for lr in para_learning_rate:
try:
#랜덤으로 초기값을 설정하는 경우
estimator = MiniSom(n,n,4,sigma =sigma, learning_rate = lr, topology='hexagonal',random_seed=0)
estimator.random_weights_init(data.values)
estimator.train(data.values,1000,random_order=True)
qe = estimator.quantization_error(data.values)
#te = estimator.topographic_error(data.values)
winner_coordinates = np.array([estimator.winner(x) for x in data.values]).T
cluster_index = np.ravel_multi_index(winner_coordinates,(n,n))
res.append([str(n)+'x'+str(n),sigma,lr,'random_init',qe,len(np.unique(cluster_index))])
#pca로 초기값을 설정하는 경우
estimator = MiniSom(n,n,4,sigma =sigma, learning_rate = lr,topology='hexagonal', random_seed=0)
estimator.pca_weights_init(data.values)
estimator.train(data.values,1000,random_order=True)
qe = estimator.quantization_error(data.values)
#te = estimator.topographic_error(data.values)
winner_coordinates = np.array([estimator.winner(x) for x in data.values]).T
cluster_index = np.ravel_multi_index(winner_coordinates,(n,n))
res.append([str(n)+'x'+str(n),sigma,lr,'pca_init',qe,len(np.unique(cluster_index))])
except ValueError as e:
print(e)
#결과 데이터프레임 생성 및 sorting
df_res = pd.DataFrame(res,columns=['map_size','sigma','learning_rate','init_method','qe','n_cluster'])
df_res.shape
df_res.sort_values(by=['qe'],ascending=True,inplace=True,ignore_index=True)
df_res.head(10)
#시각화를 위한 lineplot 생성
plt.figure(figsize=(20,10))
sns.lineplot(data = df_res)
e_time = pd.Timestamp.now()
print('\n종료시간:',e_time,'\n총 소요시간:',e_time-s_time)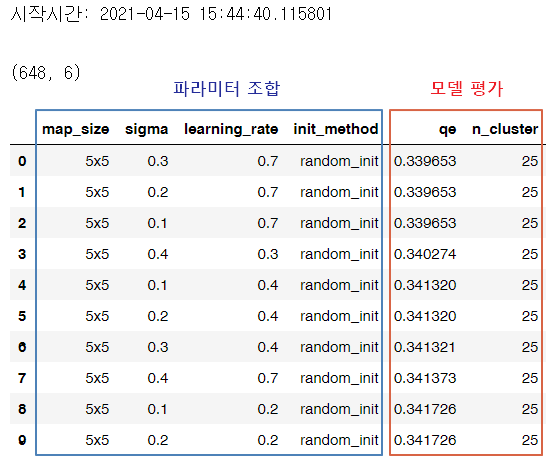
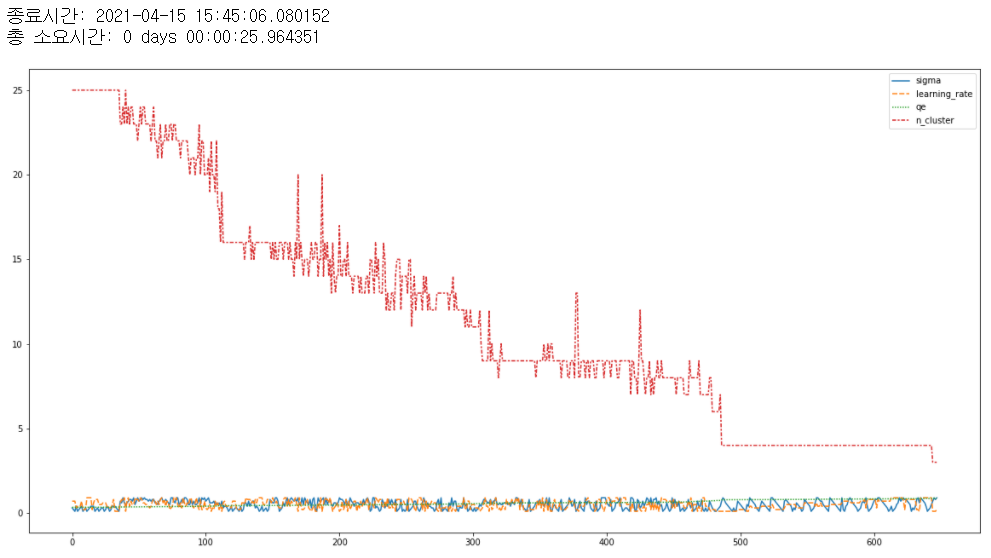
적은 수의 클러스터를 만드는 모델을 선택하고 싶어서, n_cluster가 6인 파라미터 조합으로 추린 후, qe 값이 가장 작은 조합으로 최종 선택했다.
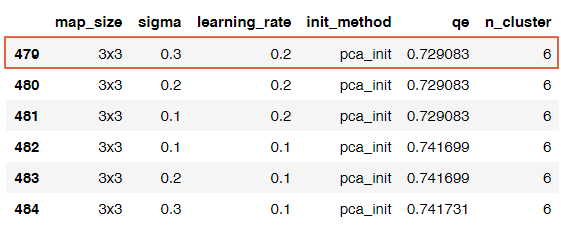
4. 모델 파라미터 조정
3단계에서 최종 선택한 파라미터로 최종 모델을 생성한다.
som_b2 = MiniSom(3,3,4,sigma=0.3,learning_rate=0.2,topology='hexagonal',neighborhood_function='gaussian',activation_distance='euclidean', random_seed=0)
#초기값설정
som_b2.pca_weights_init(data.values)
som_b2.train(data.values,1000,random_order=True)
#평가
som_b2.quantization_error(data.values)
#som_b2.topographic_error(data.values)
5. 시각화
SOM visualization에 가장 많이 쓰이는 U-matrix를 그리고, 클러스터 내 데이터 개수를 파악하기 위해 U-matrix위에 scatter plot을 그려준다.
xx, yy = som_b2.get_euclidean_coordinates()
umatrix = som_b2.distance_map()
weights = som_b2.get_weights()
f = plt.figure(figsize=(10,10))
ax = f.add_subplot(111)
ax.set_aspect('equal')
# iteratively add hexagons
# plotting the distance map as background
# 해당 셀과 다른 이웃들 간 거리를 표현, 밝을수록 가깝고, 어두울수록 멀다
for i in range(weights.shape[0]):
for j in range(weights.shape[1]):
wy = yy[(i, j)] * 2 / np.sqrt(3) * 3 / 4
hex = RegularPolygon((xx[(i, j)], wy),
numVertices=6,
radius=.95 / np.sqrt(3),
facecolor=cm.Blues(umatrix[i, j]),
alpha=.4,
edgecolor='gray')
plot = ax.add_patch(hex)
#output노드에 해당하는 클러스터 종류 및 밀도 확인
cnt=[]
for c in np.unique(cluster_index):
x_= [som_b2.convert_map_to_euclidean(som_b2.winner(x))[0] + (2*np.random.rand(1)[0]-1)*0.4 for x in data.values[cluster_index==c]]
y_= [som_b2.convert_map_to_euclidean(som_b2.winner(x))[1] + (2*np.random.rand(1)[0]-1)*0.4 for x in data.values[cluster_index==c]]
y_= [(i* 2 / np.sqrt(3) * 3 / 4) for i in y_]
plot = sns.scatterplot( x = x_, y= y_ ,label='cluster='+str(c),alpha=.7)
#클러스터에 속한 데이터 개수 데이터프레임으로 출력
cnt.append([c,len(x_)])
#클러스터별 개수를 표 형태로 출력
df_cnt = pd.DataFrame(cnt,columns=['cluster이름','개수'])
df_cnt
#x축,y축 간격 설정
xrange = np.arange(weights.shape[0])
yrange = np.arange(weights.shape[1])
plot = plt.xticks(xrange-.5, xrange)
plot = plt.yticks(yrange * 2 / np.sqrt(3) * 3 / 4, yrange)
#차트 우측에 color bar생성
divider = make_axes_locatable(plt.gca())
ax_cb = divider.new_horizontal(size="5%", pad=0.05)
cb1 = colorbar.ColorbarBase(ax_cb, cmap=cm.Blues,
orientation='vertical', alpha=.4)
cb1.ax.get_yaxis().labelpad = 16
plot = cb1.ax.set_ylabel('distance from neurons in the neighborhood',
rotation=270, fontsize=16)
plot = plt.gcf().add_axes(ax_cb)
#이미지 저장
#plt.savefig('som_seed_hex.png')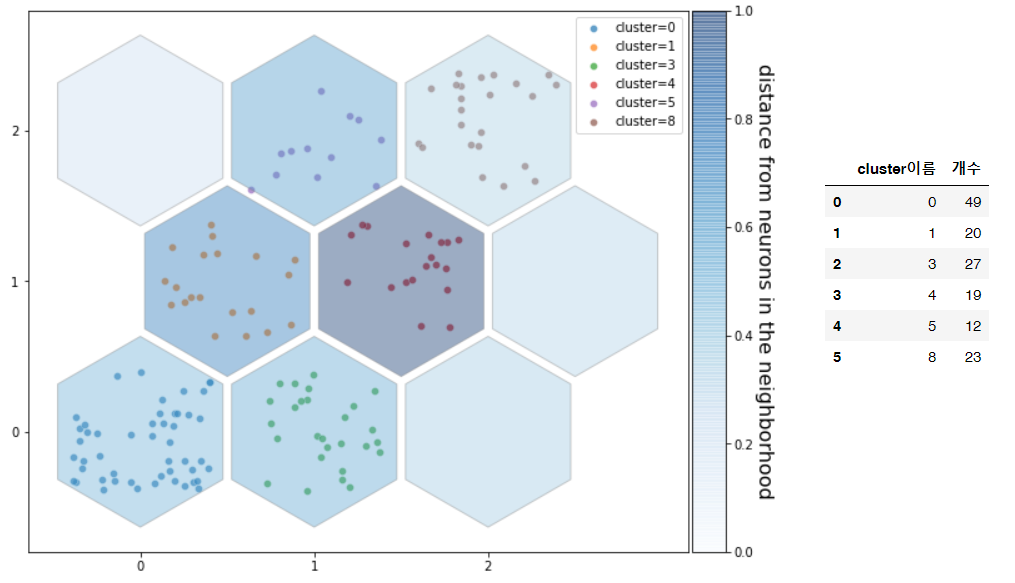
정육각형 노드의 색이 진할수록 다른 노드와 잘 구분되어 멀리 떨어져 있다는 의미이며, 노드 위의 점 개수가 많을수록 클러스터에 많은 데이터가 포함되어 있는 것이다. 위 그림에서는 1번 클러스터와 4번 클러스터가 다른 클러스터와 잘 구분되어 있음을 알 수 있다.
이외에도 2개의 설명변수 쌍을 각각 x축, y축으로 두고 scatter plot을 그려서 각 설명변수가 클러스터에 미치는 영향 (클러스터의 특성)을 파악해볼 수도 있다.
지금까지 S.O.M 알고리즘 개념과 MiniSom 패키지 활용 방법을 알아보았다. (●'◡'●)
'머신러닝' 카테고리의 다른 글
| [머신러닝] GMM(Gaussian Mixture Model) 군집화 (3) | 2021.08.19 |
|---|---|
| [머신러닝] 클러스터링 평가지표 - 실루엣 계수(2) (0) | 2021.07.21 |
| [머신러닝] 클러스터링 평가지표 - 실루엣 계수 (1) (3) | 2021.06.15 |
| [머신러닝] K-Means 군집화 (4) | 2021.05.30 |
| [머신러닝] S.O.M 알고리즘 (1) - 개념 (0) | 2021.05.04 |




댓글